
The probability that a randomly selected student receives a score between 87 and 93 is 0.2358. To find this probability, we can subtract the larger value of NORMDIST() from the smaller value of another NORMDIST() in Excel as follows: Example 3: Calculate Probability Between Two Valuesįind the probability that a randomly selected student receives a score between 87 and 93. The probability that a randomly selected student receives a score greater than 80 is 0.1587. To find this probability, we can simply do 1 – NORMDIST() in Excel as follows: Example 2: Calculate Probability Greater than Some Valueįind the probability that a randomly selected student receives a score greater than 80. The probability that a randomly selected student receives a score less than 80 is 0.1587.
#CALCULATING NORMAL DISTRIBUTION PERCENTAGES IN EXCEL HOW TO#
The following screenshot shows how to use the NORMDIST() function in Excel to calculate this probability: Suppose the scores for an exam are normally distributed with a mean of 90 and a standard deviation of 10.įind the probability that a randomly selected student receives a score less than 80. Example 1: Calculate Probability Less than Some Value

The following examples show how to use this function to calculate probabilities related to the normal distribution.
cumulative: Whether to calculate cumulative probabilities (this is usually TRUE).standard_dev: The standard deviation of the normal distribution.mean: The mean of the normal distribution.x: The value of interest in the normal distribution.Look up a probability and find the z-quantile.
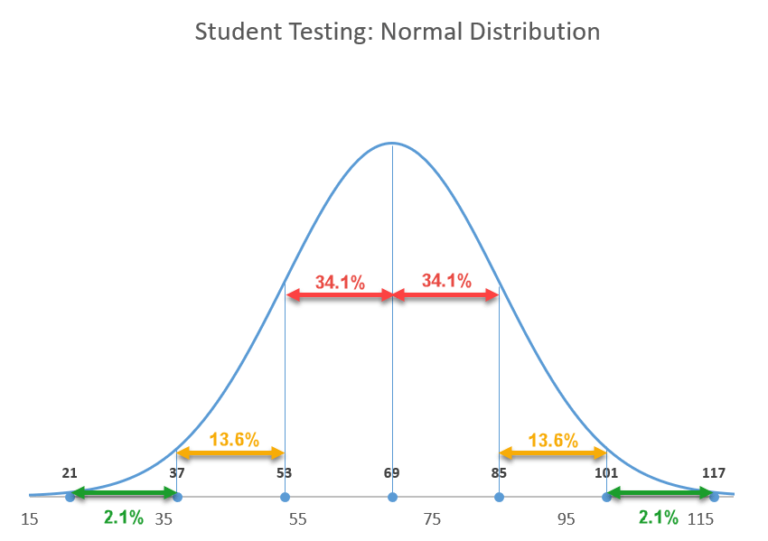
Calculate a z-score and find the probability under the curve. The Z-table assumes a mean of 0 and a standard deviation of 1 (hence why we calculate a z-score before going to the table). To calculate probabilities related to the normal distribution in Excel, you can use the NORMDIST function, which uses the following basic syntax: =NORMDIST(x, mean, standard_dev, cumulative) You shouldnt be getting the standard deviation or the mean from a Z-table. A normal distribution is the most commonly used distribution in all of statistics.


 0 kommentar(er)
0 kommentar(er)
